Type-2 Fuzzy Number-Based Intuitionistic Fuzzy Interpolation Bezier Curve Modeling

Abstract

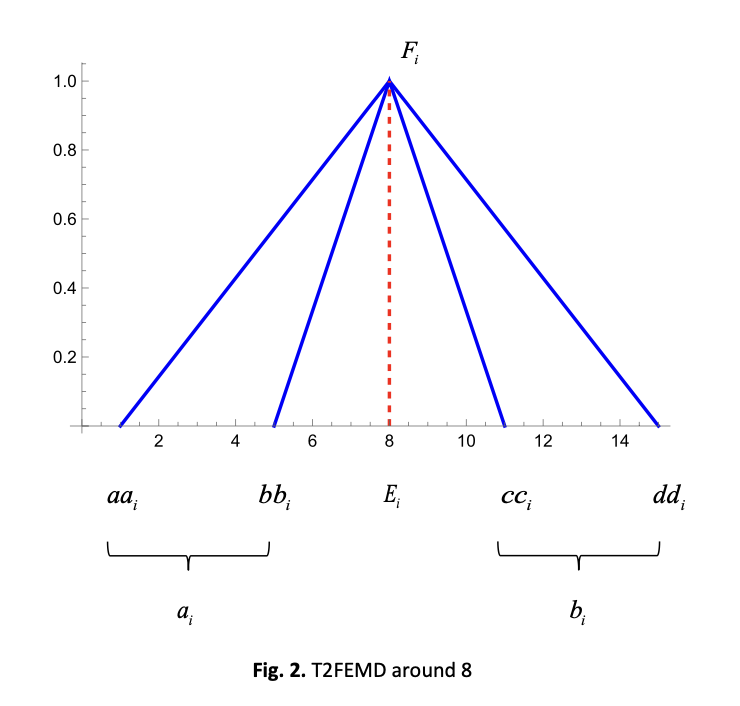
The challenge is to accurately evaluate uncertainty in imprecise data in complicated systems, particularly when the data is subjective or based on measurements that are very inaccurate. This paper shows a new method of accomplishing things by using a Bézier curve interpolation framework with Type-2 fuzzy numbers (T2FNs) and intuitionistic fuzzy sets. The T2FN based Intuitionistic fuzzy interpolation Bézier Curve that is being spoken about here exhibits uncertainty in two ways which are via secondary membership functions and hesitation degrees. This is great for data that is highly unclear. The way the construction is done mixes the flexibility of Bézier curve geometry with the more expressive T2FN and intuitionistic fuzzy notions. We test the model with both fake and genuine data, including earthquake magnitude data that fluctuates a lot. The experiment's results suggest that the T2FN-IFIBC is superior at handling data uncertainty because it makes curve fitting more stable and adaptable. When faced with ambiguous data, this technique empowers the maximization of the potential of geophysical modeling, risk analysis, and data analytics, enabling the achievement of extraordinary results.