Magneto-hydrodynamic Scrutiny of Thermal Stratification in a Self-similar Casson-Walter-B non-Newtonian Fluid over a Porous Vertical Plate

Abstract

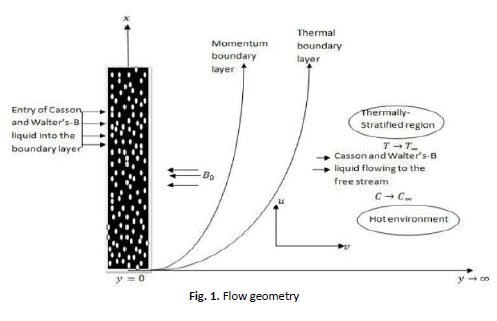
Thermal stratification of magneto-hydrodynamic self-similar Casson-Walters-B non-Newtonian fluids past a porous vertical plate is explored in this paper. The occurrence of this nature is plausible in industrial processes such as polymer industries. The numerical investigation in this paper is a binary solution which consists of Casson and Walters-B type of fluids. The flow equations that govern the study are nonlinear coupled partial differential equations (PDEs). These sets of PDEs were evaluated using suitable variables to obtain nonlinear ordinary differential equations (ODEs). The set of transformed ODEs were solved numerically by employing the spectral homotopy analysis method (SHAM). SHAM combines the Chebyshev pseudospectral approach with the homotopy analysis method in solving set of differential equations. From the physical point of view, the significance of each pertinent flow parameters are discussed with the help of graphical results. It was found that the plastic dynamic viscosity greatly affect the velocity of Casson fluid within the boundary layer. In the thermally-stratified boundary layer, the magnetic parameter was found to slow down the motion of an electrically conducting fluid due to Lorentz force. The rate of heat transport was determined by pertinent flow parameters such as thermal radiation, viscous dissipation, and heat generation. For exampled, thermal radiation becomes very significant at a very high temperature, and viscous dissipation in firctional heating of fluid particles. The validation conducted in this paper shows the accuracy of SHAM. The comparison of the present results are previously published works are in good agreement.