Analytical Study of Non-Newtonian Magnetic Casson Blood Flow with Gold Nanoparticles through an Inclined Stenosed Artery

Abstract

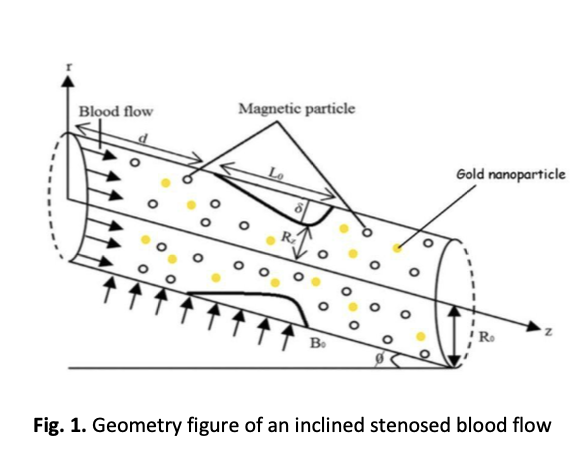
This study presents a mathematical model of non-Newtonian Casson blood flow in an inclined stenosed artery with the inclusion of gold nanoparticles. The governing fractional differential equations are formulated using the Caputo-Fabrizio fractional derivative without a singular kernel. The blood flow was modelled under the influence of a uniformly distributed magnetic field and an oscillating pressure gradient for both blood and magnetic particles velocity profiles. The analytical solutions were obtained using Laplace and finite Hankel transforms. These distributions are presented graphically using Mathcad software to analyse the effects of various physical parameters. To validate the results, the obtained solutions in limiting cases were compared with previously published findings and showed good agreement. The analysis reveals that the velocities of both blood and magnetic particles of both blood and magnetic particles increase with increasing fractional parameter, Casson parameter and time, whereas both velocity decrease as the Hartmann number increase. This model provides valuable insights into the hemodynamic behaviour of blood flow, particularly in understanding and treating cardiovascular diseases such as atherosclerosis.